(This is the fourth in a series of posts looking at high-speed video of intro physics scenarios. The others involve eddy currents, falling slinkies, and dropping springs.)
One of my favorite weird student course evaluation comments of all time was from a long-ago student who wrote something along the lines of “The classes were fine, but the course abstracted away all the interesting forces, like air resistance and friction…” This is funny to physics professors, because there are a ton of jokes about intro problems where the punch line is “…neglecting air resistance.”
The reason for this is simple: if you want to solve problems with just pencil and paper, friction and air resistance make that nearly impossible. We talk about those forces a little bit, but what little we do present takes the form of quasi-empirical approximations that mostly work all right, provided you don’t push them too far. (See, for example, the recent-ish post about baseball that set me off on this summer of physics blogging.) They do, however, have mathematical properties that lend themselves to the writing of relatively straightforward problems.
We do recognize this as a limit, though, and in an effort to introduce a little more realism into our curriculum, have started doing a “coffee filter drop” lab at some point in the term. This is pretty much what it sounds like: You have one person stand in a high place, drop one of those conical-ish coffee filters, and watch it fall to the ground. Like this:
The filter’s mass is small enough that it is affected very significantly by air resistance— you can see it fluttering a bit in the video. The conical shape of the filter keeps it a bit closer to a constant orientation than you would get from a sheet of paper, say, so it’s a little easier to track than it otherwise might be.
And, importantly, these are designed to stack with each other, so you can drop a stack of multiple filters and it will have almost the same aerodynamic properties as the single filter. This is important because our quasi-empirical approximation for air resistance forces depends on the surface area and shape of the moving object. A consistent shape and orientation means that the only thing changing as you stack more filters is the mass, which is the kind of nice single-independent-variable experiment we like to do in physics.
What does changing the number of filters do, though? Well, it increases the force of gravity on the filter stack. You might not think this matters, having learned as a small child that all objects fall at the same rate near the surface of the Earth— Galileo apocryphally dropping balls off the Leaning Tower of Pisa and all that— but that’s only true neglecting air resistance. When you add in air resistance, the downward acceleration of the ball is determined by the net force, the weight due to gravity minus the upward force of air resistance— and it changes in time.
This leads to the phenomenon of terminal speed, which I describe for the coffee filter lab using the following slide:
When first released, the filter isn’t moving so there’s no motion for the air to resist and the acceleration will be close to the normal acceleration of gravity. As it picks up speed, the air resistance force increases, and thus the acceleration decreases. At some particular speed, the air resistance force exactly matches the force of gravity, and the object stops accelerating. From that point on, it moves downward at a constant speed (the “terminal speed,” in physics jargon). That speed will depend on the mass— the heavier the object, the longer it keeps accelerating, and the higher the speed.
So, when we drop different stacks of filters, we can measure the terminal speed for a variety of different masses, and see whether that agrees with what we would predict from the quasi-empirical approximation for the air resistance force. In class, we do this by having students time the fall of the filter stacks: they drop the stack from up near the ceiling, and measure how long it takes them to fall the last meter or so. This assumes that the filters have actually reached their terminal speed by that point, which seems to be basically okay; at least, the results we see in the intro labs more or less agree with what you’d predict for how the terminal speed should depend on the mass.
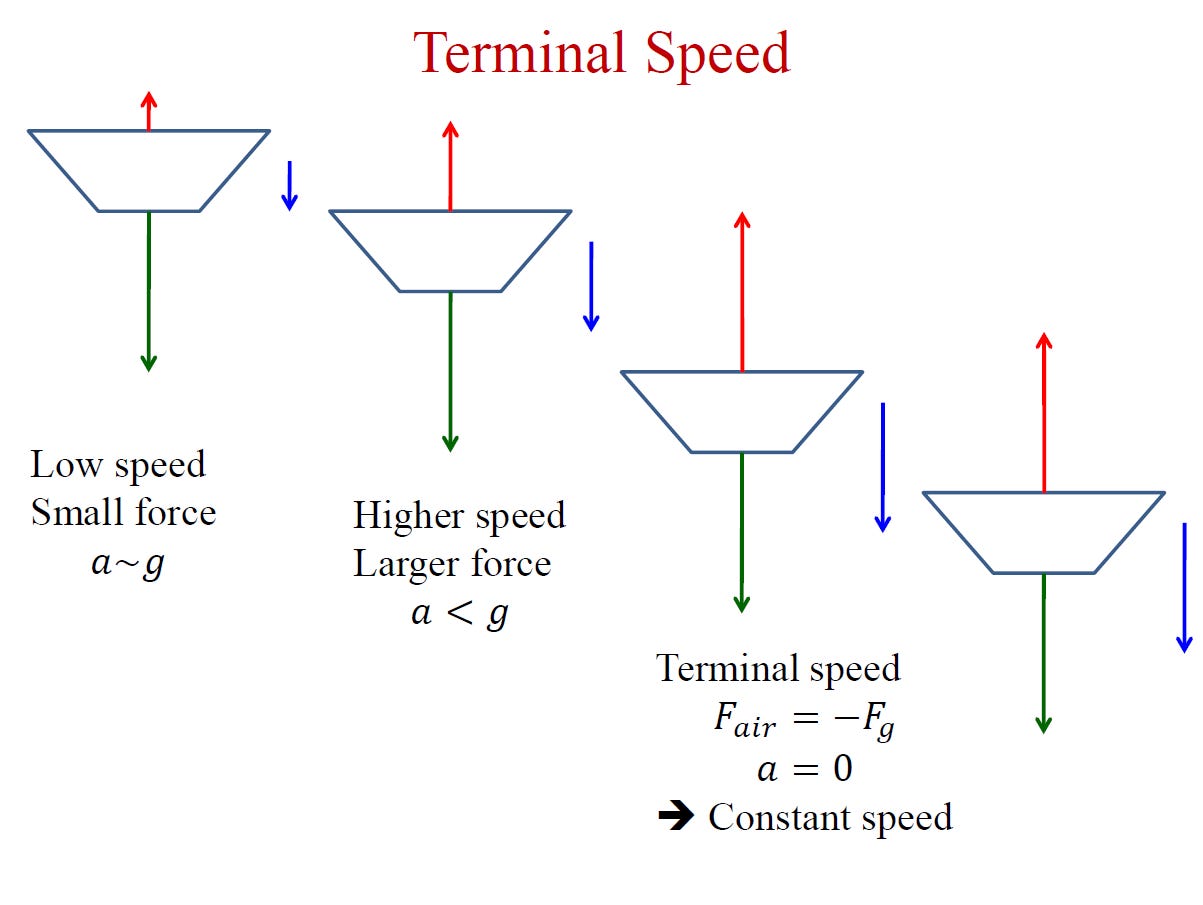
But, you know, we have this fancy high-speed video camera, so why not look at this in a bit more detail? The clip above shows a single filter being dropped, filmed at 250 frames per second. I repeated this for a whole bunch of filter stacks, leading to the following graph:
This shows the position of the falling filter as a function of time, and qualitatively does the thing you would expect: small stacks take a long time to reach the ground, big stacks fall much faster. You could, in principle, fit functions to these to determine all the properties, but it’s a little more illuminating to think about this in terms of the velocity as a function of time, and the auto-tracking feature of Tracker Video Analysis does a decent enough job with these images, so here’s that plot:
Again, you see qualitatively the right behavior: light stacks accelerate at the start and then quickly level off to a nearly constant speed, and heavier stacks accelerate more and take longer to settle in. The two heaviest stacks here, 12 and 16 filters, probably haven’t reached their terminal speed by the time the graphs cut off because they hit the floor.
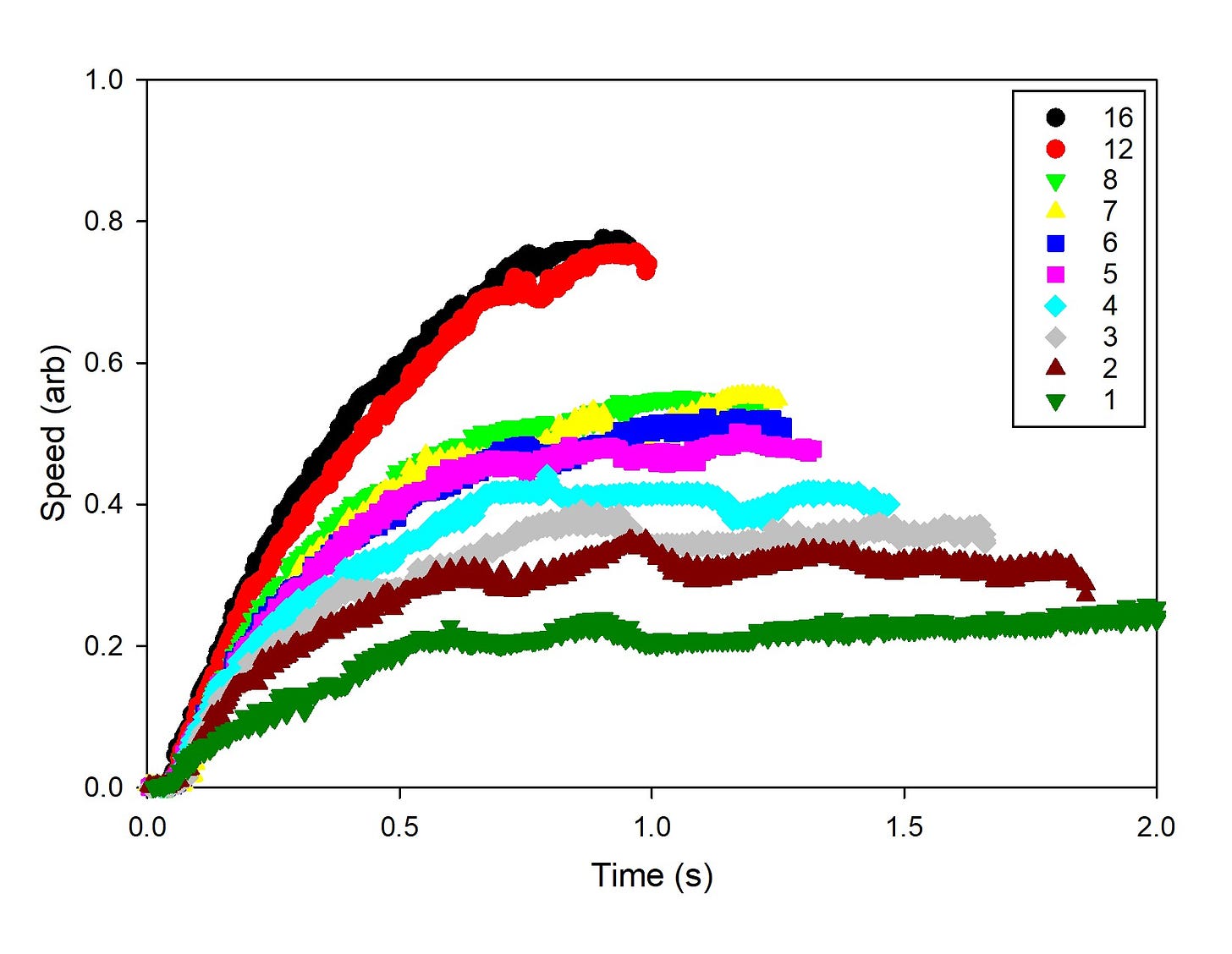
This looks slightly odd because of the way that the data cut off when the filter stack reaches a particular height. It’s maybe a little more aesthetically pleasing to plot this as speed vs distance, which looks like this:
(I cut down the number of runs plotted to just the powers of two, because it’s a cleaner visual…) This is a little trickier to interpret in a formal mathematical sense (what the slope means isn’t as clear), but gets the right idea: larger stacks lead to acceleration that continues for more of the drop, and a higher terminal speed.
So, is this a big improvement over the “time the last meter of fall” thing we do in the lab? Enh. The result we would expect from the usual approximation is that the terminal speed increases like the square root of the number of filters, and that’s mostly true— the 16-filter stack is about four times as fast as the single filter— but it’s not all that great. I did some fits to extract the terminal speed, and the square-root fit is not a whole lot nicer than what we get in the intro lab.
How could this be made to work better? Well, there are two basic issues. The first is that the heavier stacks don’t really reach terminal speed in just a couple of meters of fall. That could be addressed by dropping from a greater height— if I moved the setup out into the atrium of the building, it would be relatively straightforward to double the drop height, and that would probably give better results. That’s a bit of a hassle, though, because the auto-tracking needs a pretty consistent image, so we’d need to drape a big curtain as a backdrop, or some such.
The second issue follows directly from that, which is that while the conical-ish shape of the filters helps keep the orientation of the falling filter stacks consistent, it’s not perfect. Which creates some noise in the auto-tracking data, as the apparent shape evolves. The solution to this would be to use something that’s more visually uniform, but then it’s harder to change the mass. If I were to carry this further, I think I’d look into 3-d printing some plastic spheres of the same radius but different masses, or maybe a really light hollow sphere with a way to insert masses in the center. That would likely give cleaner data from the auto-tracking, which in turn might lead to cleaner terminal speeds. Probably some combination of the two would be the best way to go.
We are, however, rapidly running out of summer, and I need to shift my energy toward preparing for the Fall term, so this is a project for another time. Maybe next summer, or the December break, we’ll see…
So, that’s a little less conclusive than I would like. But, you know, you can’t win ‘em all… If you want to see when and if I follow this up, here’s a link:
And if you feel so moved, the comments will be open:


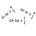


Hollow spheres with different masses... that sounds familiar!
https://en.wikipedia.org/wiki/1980_Pennsylvania_Lottery_scandal