The news has, incredibly, gotten even more stupid and annoying over the last week, providing even more incentive to putter around in the teaching labs using high-speed video to look at basic physics. Last week’s post about eddy currents wasn’t something I’ve seen done a whole lot, but this week is a classic: the ever-popular Slinky Drop.
The key idea here is that if you take a long and stretchy spring and suspend it from the top, let it settle in for a bit, then suddenly release it, the top end will immediately start falling, but the bottom won’t move until more or less the entire spring above it has relaxed. In high speed (500 fps, give or take), it looks like this:
This is rigged up so I can do it by myself— the slinky is suspended from a spring over a pulley so I can release it from a point closer to the camera, and not need to wait for it to settle to equilibrium before dropping. You can clearly see the qualitative behavior in the video— the top starts moving, but the bottom doesn’t.
The way to understand this is that each short segment of spring exerts an upward force on whatever is below it that depends on the stretch of the segment, and experiences downward forces from both gravity and the segment below it. When the spring is hanging from the support, this is all ultimately tied to an immovable object exerting a force that it equal to the weight of the whole thing, so nothing goes anywhere. When that force is removed from the top segment, it starts to accelerate downward immediately, but continues pulling up on the segment below it until it has returned to its relaxed state. At which point the second segment starts to accelerate downward, but continues pulling up on the third segment until it has returned to its relaxed state, and so on.
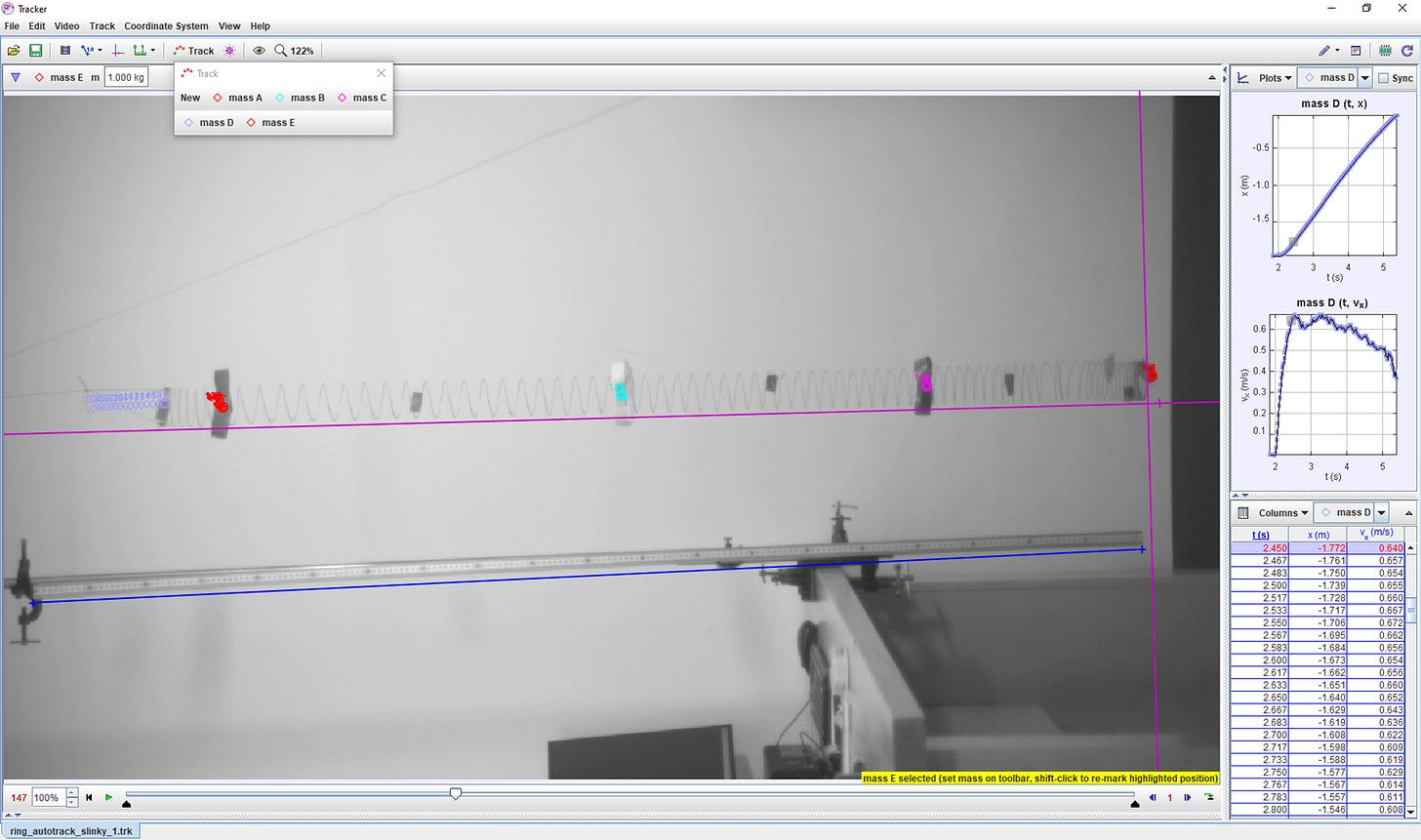
You can do all kinds of mathematical modeling of this, but my personal inclination is more experimental: I want to see what kind of quantitative data I can extract from video of a drop, so I cranked this into Tracker and went to work:
Actually, most of the work here was in making the video. Or, to be more precise, making the right video. At 500 frames per second, there’s a lot of data even for a very fast drop— a little over 200 points— and I wanted to be able to measure the behavior of several different points on the spring. Which means I very much did not want to have to manually mark the position of multiple points in each of 200-odd frames. Which meant getting the Autotracker feature to work properly.
I initially thought this would be a simple matter of putting bits of tape at intervals, but that doesn’t work very well. The autotracking feature is essentially an image-matching algorithm, and small bits of tape change too much for it to keep following them. The spring tends to twist as it falls, changing the size and shape of the tape in the image, and even when it doesn’t, as the spring relaxes, the tape doesn’t stand out against the collapsed stack of coils as clearly as it does when the spring is stretched.(The high-speed camera is monochrome, so the bright red gaffer tape doesn’t stand out as clearly against the grey metal of the spring as I would like...)
My second thought, visible in the wide shot at the very top of this post, was to use something that sticks out from the sides— plastic straws from my local Starbucks, in this case— so they’d be clear of the stack. These still had a twisting problem, though, and additionally tended to flex up and down as the drop reached them, adding a bunch of spurious “motion” to the ends.
What finally worked was using gaffer tape to make circular loops a bit bigger than the slinky, and fixing those on with a bit of scotch tape. being circular, they maintained a more constant appearance when the spring twisted, and being a bit wider, they still stuck out a little. That combination was enough to get the following auto-tracked data for five spots on the spring (the very top and bottom, and three tape rings in the middle):
You can see that the marked points barely change position until the segments above them just about reach their position, at which point they start dropping to match whatever’s coming down from above. You can barely see any motion from the very bottom, because it very quickly falls down against the dark baseboard and the image tracking loses it, but it does drop slightly.
One of the really nice features of getting this tracked automatically is that the data for velocity as a function of time is not unreasonable:
If you mark the points manually, there’s inevitably enough error from guessing and pixelation that the speed is super noisy, but this isn’t half bad, and totally justifies all the fiddling I did with different ways to make the autotracker work. You see the same pattern here: basically zero velocity until the descending stack gets very very close, and then a rapid acceleration up to match the speed of the falling stack.
If you look at that velocity data, you see that there’s a distinct downward slope to the speed of the merged segments— they’re moving downward, but also slowing down very slightly. That might seem counter-intuitive, given that they are, in fact, subject to a constant force of gravity pulling them down, which usually causes the speed of a falling object to increase with time. So, why does the falling spring seem to be slowing down?
The way to understand this is that if you zoom out, you would expect the spring as a whole to accelerate under the influence of gravity. That is, the center of mass of the spring should fall like a single mass, accelerating downward at 9.8 m/s/s. whatever the individual segments are doing needs to add up to that, which means that in the early stages where only a few coils of the spring are moving, they can be going faster than you would expect (pulled down not just by gravity but by the force of the stretched spring below them), but as a larger and larger fraction of the whole is moving, the speed has to look more like what you expect for the center of mass.
I know how many turns of spring are between the markers I put on the hanging slinky, so I can use the position data to construct the center-of-mass of the whole thing, basically by assigning each section to a center-of-mass position midway between two tracked positions, with a mass equal to however many turns of spring are between them, then using those to find the overall center of mass of the spring. That center-of-mass position looks like this:
The blue dots are the calculated center of mass for the whole spring, the reddish line is a parabola fit to the data. The acceleration of this is 9.32 m/s/s, which is remarkably good for such a crude experiment. So, you know, physics works!
There are still some funny details here, like the way the center-of-mass position is visibly segmented, corresponding to how many of the sections are moving at any given time. This is probably an artifact of the way I did the calculation, which puts the center of mass of each section of spring at the midpoint between two markers. That’s probably a good approximation when the spring is collapsed, but less so when it’s stretched, and that shift might well lead to the segmenting you see in the graph. I’m honestly a little amazed that it worked as well as it did, though…
The one big refinement I would make if I were trying to do a better job here would be to get more range after the spring is fully collapsed, so see it change over to falling as a single object accelerating under gravity. As it it, the spring starts to disappear into the baseboard very soon after the collapse reaches the bottom. This is just a matter of the camera lenses and the size of the room— I couldn’t get it to focus clearly with a view any wider than what you see in the clip above, so there’s not really room in the frame for more of a drop. It’s probably possible to move furniture around and get the camera a bit father away, allowing more of a drop, but at the end of the day, I’m doing this for my own amusement, and don’t care that much.
And this was, in the end, a pleasant and amusing diversion for me, puttering around in the lab. I hope it’s something of the same for you to read.
This was the other big video-analysis lab from my Spring term class that I wanted to re-do; I’m not sure I have a great plan for any of the rest. I might come up with something, though; if you want to see what that is if and when it happens, here’s a button:
And if you want to suggest anything, the comments will be open:







This is fascinating to see. I'd love to sit down and think through the impact of the discontinuous spring constant and energy loss - the relaxed state of the slinky is collapsed, with all the coils in contact, so it can't really oscillate about a neutral position. If you just let the bottom of the slinky sit on the floor, holding the top above, and drop it, it doesn't bounce back to the height you let it go; it hardly bounces back at all - a lot of the potential energy and deformation energy are getting lost. If you took a more "physics-y" spring, you could superimpose the oscillatory motion of any point on the spring with the rigid body motion under gravity. Although you couldn't treat the mass of the spring as negligible in the oscillatory solution like you would with a more traditional spring/mass problem....