Annoying Problems Turned Ingenious Solutions
And how some very cool physics can make me feel old...

Over at Physics, they have an article up about a new paper from Jun Ye and collaborators at JILA in Boulder on the latest and greatest improvements in their strontium atomic clock. This was brought to my attention by Brian Keating over on ex-Twitter (slightly ahead of the weekly email direct from the journal…), and as I noted in reply, this is a paper that both is very cool and makes me feel old.
The “very cool” part is just the technical result: they’ve taken what was already an impressive frequency standard, doing ultra-precise spectroscopy to determine the exact frequency of light associated with a transition between two energy states in strontium, and made it even better, by about a factor of two. The custom in hyping these is to quote a ridiculous huge value for the time it would take for this to accumulate a one-second timing error (that is, if you built two of these and ran them continuously as clocks, how long would it take before they disagreed by one second). In this case, that’s 39.6 billion-with-a-B years, which is pretty crazy.
The actual process by which this was accomplished is nothing especially revolutionary, it’s just a matter of being really astonishingly good and careful about precision metrology. They spent a huge amount of effort on both experiment and theory to nail down various systematic effects that add uncertainty to the frequency they measure, and account for them. It’s fascinating if you’re a huge nerd about this kind of stuff, but also highly technical and not super interesting to explain.
The “makes me feel old” part, on the other hand, is much cooler. It has to do with the key enabling technology behind these systems, which is the “magic wavelength optical lattice.” This is really cool as an example of experimental ingenuity turning what would ordinarily be an annoying problem into a fabulous opportunity. And that’s worth a little bit of unpacking here.
To understand the problem and the process, we need to back up a bit and talk about the core idea behind atomic clocks, namely that atoms have discrete energy states (represented by the horizontal lines in the cartoon diagram above) and move between them by absorbing and emitting light. If you tune the light to a frequency that perfectly matches the energy spacing (the double-headed green arrow in the leftmost panel of the cartoon diagram), the atoms will flip back and forth between states in a very regular way, and you can use that “Rabi flopping” to nail down the frequency of the light extremely well. Then you turn that into a clock, by counting the oscillations of the light as the “ticks” by which you measure time.
This is complicated a bit by the “light shift,” illustrated by the next two panels of the cartoon. If you shine light on an atom that is close to but not quite exactly at the frequency the atoms want to absorb, the result is not as simple as them simply failing to absorb the light. In fact, the presence of the light perturbs the internal states, in a way that depends on which way the frequency is off. If the light has a “red detuning,” a frequency that’s a little too low (smaller energy than the bare atom is looking for), the states push apart: the lower-energy one decreases in energy, and the higher-energy one increases in energy. For a “blue detuning,” the opposite happens: the lower state moves up, and the upper state moves down.
This is the first bit of experimental ingenuity, as the light shift is the basis for the technology of the “optical lattice” in general. If you illuminate a collection of atoms with a pattern of light that’s brighter in some places than others, that intensity pattern turns into a pattern of energy shifts: there will be places where the energy of an atom in the lowest-energy state (which it’s not hard to ensure that most of them are) is lower. And since everything in the universe “wants” to be in the lowest-energy configuration available, the atoms in a sample will tend to end up at those low-energy positions, trapped in a small region around the minimum energy locations. It’s really easy to make an array of these: a line of places where atoms get trapped, spaced by half the wavelength of the light used to shift the states. This looks a lot like the crystal lattice of atoms seen by electrons in a solid, but it’s created by the light, thus “optical lattice.”
This is a great way to collect significant numbers of atoms at ultra-low temperatures and hold them in place, which seems like a great basis for a clock. Except, that picture is a little too simple: it’s based on idealized two-level atoms. And, to paraphrase a famous misquote of Bill Phillips, in the real world there are no two-level atoms, and strontium is not one of them.
Real atoms have many more than just two energy states, so if you want to think about how they respond to light, you need to account for all of them, represented by the second panel from right in the cartoon above. In figuring out what the various energy states do, you need to think about the effect of the light on each and every one of those states in relation to each of the others. Loosely speaking, you need to think about all the possible states the light might try to move the atom to, some of which will be trying to push the energy of the state you’re starting in up, while others try to push it down.
This plays hell with any attempt to use atoms in a lattice as a clock, because the upper and lower states shift in different ways, making the exact frequency depend on the details of the lattice field you’re using to confine them. You can sorta-kinda avoid the problem by turning the lattice light off when you want to do really precise measurements, but when you turn the light off, the atoms aren’t confined any more and start flying away, which is not a great feature for a clock.
The ingenious solution to this problem is the “magic wavelength”: under the right conditions, you can find a particular wavelength of light for which the shift of the upper clock state and the lower clock state are exactly the same. The up and down pushes from all the places the light might send an atom starting in the lower state add up to a particular downward shift in the energy, and the up and down pushes on the upper energy state for the clock add up to exactly the same downward shift. That means that for a lattice generated by this one particular wavelength of light, the frequency of the internal clock doesn’t change as you move around: every atom has the same energy level difference, whether it’s in the light or not.
The “magic wavelength lattice” is thus doubly ingenious: it’s using the light shift (which otherwise is a systematic problem for making an atomic clock) to trap atoms, and it’s exploiting the multi-level nature of the atoms to cancel out the energy shifts and let you keep the atoms in the lattice while you use them in the clock. This is why the last several rounds of “best atomic clock in the world” have mostly involved optical lattice clocks. (The alternative approach is to use trapped ions; these are also incredibly clever, in a different way…)
What’s the “make me feel old” part of this? It’s that I remember the first discussion of the “magic wavelength” idea in the context of optical lattices and atomic clocks. In 1998, when I visited the lab of Hidetoshi Katori at the University of Tokyo. Which, as my kids rejoice in reminding me, was near the end of the previous century.
When I was in Japan, Katori had just come up with the idea, and was demonstrating it not in a lattice but just with laser cooling— showing that he could trap strontium atoms with one frequency of laser light, and cool them to exceptionally low temperatures with a different one. I was blown away, but thought “Well, that’s just incredibly lucky…” But it turns out to be a pretty general phenomenon: whatever element you’re interested in, you can probably find a “magic wavelength” for some pair of states that leaves their energy difference unchanged (whether that will be at a convenient frequency to work with is another matter…). A couple of years later, I ended up chairing a session at a conference in France where he presented about it; he was the last speaker, and we let his talk and the Q&A go on well into the meal break, because it was such a neat idea.
And now, it’s a solidly well-establish piece of the experimental AMO physics toolkit, to the point where even relatively general-audience stories don’t really feel compelled to explain it. And younger physicists kind of look sideways at me when I enthuse about how cool the whole thing is, since they just take it for granted. It’s the same “Okay, boomer…” face I get from my kids when I mention some bit of pop culture ephemera from “the late 20th century”…
So: Very clever physics, that also make me feel old, because I was there when it first appeared.
A nice bit of nostalgia, and also scratching a bit of the “explain some physics” itch. If you want to see whether I produce more of this or slide back into politics, here’s a button:
And if you have questions or want to point out problems with my highly simplified explanation, the comments will be open:


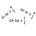


The image produced by A.I. looks more like what John Harrison would've built, hahaha. So, still impressive, I guess... just kidding.
I studied physics as an undergrad, but ended up in engineering. I'm even older than Chad, so my physics days were a loong time ago. Even so, I find this kind of thing fascinating, and, well, cool!